If a Bus Suddenly Stops the Driver s Body Continues to Move Forward
If the moving bus suddenly stops, why do passengers fall in the forward direction?
A passenger sitting in a moving bus is in motion. When the bus suddenly stops, the lower part of our body is brought to rest along with the bus whereas upper part continues to be in motion due to inertia of motion and hence falls forward.
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
(i) A, (ii) B along the direction of string.
What is the tension in the string in each case?
Horizontal force,F = 600 N
Mass of body A, m 1 = 10 kg F =ma Acceleration (
Mass of body B, m 2 = 20 kg
Total mass of the system, m = m 1 + m 2 = 30 kg
Using Newton's second law of motion,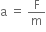
=
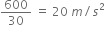When force is applied on a body A.
Equation of motion can be written as,
F - T = m1a
Therefore,
T = F - m1a
= 600 - 10 x 20
= 400 N ... (i)
When Force is applied on a body B, we have
F - T = m2a
i.e., T = F - m2a
Therefore,
T = 600 - 20 x 20 = 200 N ... (ii)
From (i) and (ii), we can say that the answer is different in both the cases.
Therefore, the answer depends on which end of mass, the force is applied.
Figure 5.16 shows the position-time graph of a particle of mass 4 kg. What is the (a) force on the particle for t < 0, t > 4 s,0 < t < 4 s? (b) impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only).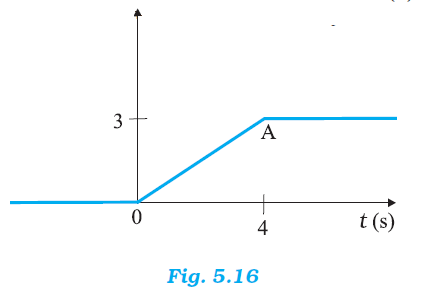 
From the given graph, the position of the particle is coincident with the time axis. That is, the displacement of the particle in this time interval is zero. Hence, the force acting on the particle is zero.
Fort > 4 s
In the given graph, the position of the particle is parallel to the time axis. It indicates that the particle is at rest at a distance of 3 m from the origin. Hence, no force is acting on the particle.
For 0 < t < 4 Hence, the acceleration produced in the particle is zero.
The position-time graph has a constant slope in the given graph.
Therefore, the force acting on the particle is zero.
(b) Att = 0, = 3 kg m/s
Impulse = Change in momentum
= mv – mu
Mass of the particle, m = 4 kg
Initial velocity of the particle, u = 0
Final velocity of the particle, v =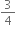
m/s
∴ Impulse = 4 x (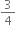
- 0)
Att = 4 s,
Initial velocity of the particle, u =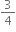 
m/s
Final velocity of the particle, v = 0
∴ Impulse = 4 (0 -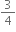 
) = -3 kg m/s
It can be observed from the given graph that the position of the particle is coincident with the time axis. It indicates that the displacement of the particle in this time interval is zero. Hence, the force acting on the particle is zero.
Fort > 4 s
It can be observed from the given graph that the position of the particle is parallel to the time axis. It indicates that the particle is at rest at a distance of
3 m from the origin. Hence, no force is acting on the particle.
For 0 < t < 4
It can be observed that the given position-time graph has a constant slope. Hence, the acceleration produced in the particle is zero. Therefore, the force acting on the particle is zero.
(b) Att = 0
Impulse = Change in momentum
= mv – mu
Mass of the particle, m = 4 kg
Initial velocity of the particle, u = 0
Final velocity of the particle, v =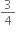 
m/s
∴ Impulse = 4 (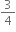 
- 0) = 3 kg m/s
Att = 4 s,
Initial velocity of the particle, u =m/s
Final velocity o9f the particle, v = 0
∴ Impulse = 4 (0 -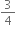 
) = -3 kg m/s
A man of mass 70 kg stands on a weighing scale in a lift which is moving,
(a) upwards with a uniform speed of 10 m s–1,
(b) downwards with a uniform acceleration of 5 m s–2,
(c) upwards with a uniform acceleration of 5 m s–2.
What would be the readings on the scale in each case?
(d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
(a)Mass of the man,m = 70 kg
Acceleration, a = 0 = 700 N = =
Using Newton's second law of motion, we can write the equation of motion as,
R – m g = ma
where, ma is the net force acting on the man.
As the lift is moving at a uniform speed, acceleration a = 0
∴ R = m g
= 70 × 10
Therefore, reading on the weighing scale =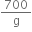 
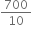
(b) Mass of the man, m = 70 kg = 70 × 5
Acceleration, a = 5 m/s 2 , downward
Using Newton's second law of motion, we can write the equation of motion as: R + m g = ma
R = m (g – a )
= 70 (10 – 5)
= 350 N
∴ Reading on the weighing scale = 350 g =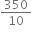 
= 35 kg
(c) Mass of the man, m = 70 kg = 70 × 15 Reading on the weighing scale = = = 105 kg
Acceleration, a = 5 m/s 2 upward
Using Newton's second law of motion, we can write the equation of motion as:
R – m g = ma
R = m (g + a )
= 70 (10 + 5)
= 1050 N
Therefore, 
(d) When the lift moves freely under gravity, acceleration a = g = 0
Using Newton's second law of motion, we can write the equation of motion as,
R + m g = ma
R = m (g – a )
= m (g – g)
∴ Reading on the weighing scale = 
= 0 kg
The man will be in a state of weightlessness.
A helicopter of mass 1000 kg rises with a vertical acceleration of 15 m s–2.
The crew and the passengers weigh 300 kg.
Give the magnitude and direction of the,
(a) force on the floor by the crew and passengers,
(b) action of the rotor of the helicopter on the surrounding air,
(c) force on the helicopter due to the surrounding air.
Given,
Mass of the helicopter, mh = 1000 kg
Mass of the crew and passengers, mp = 300 kg
Total mass of the system, m = 1300 kg
Acceleration of the helicopter,a = 15 m/s2Using Newton's second law of motion, the reaction forceR,
R –m pg = ma
=m p(g + a)
= 300 (10 + 15)
= 300 × 25
= 7500 N
The reaction force will be directed upwards, the helicopter is accelerating vertically upwards.
According to Newton's third law of motion, the force on the floor by the crew and passengers = 7500 N, directed downward.
(b)
Using Newton's second law of motion, the reaction forceR'experienced by the helicopter can be calculated as,
R' -mg =ma
=m(g + a)
= 1300 (10 + 15)
= 1300 × 25
= 32500 N
The reaction force experienced by the helicopter from the surrounding air is acting upward. Hence, as per Newton's third law of motion, the action of the rotor on the surrounding air will be 32500 N, directed downward.
(c) The force on the helicopter due to the surrounding air is 32500 N, directed upwards.
A stream of water flowing horizontally with a speed of 15 m s–1 gushes out of a tube of cross-sectional area 10–2m2, and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water, assuming it does not rebound?
Given,
Speed of the water stream,v = 15 m/s
Cross-sectional area of the tube,A = 10–2 m2
Volume of water coming out from the pipe per second,
V =Av
= 15 × 10–2 m3/s
Density of water,ρ = 103 kg/m3
Mass of water flowing out through the pipe per second =ρ ×V
= 150 kg/s
The water strikes the wall and does not rebound.
Therefore, according to Newton's second law of motion,
Force exerted by the water on the wall,
F = Rate of change of momentum =
=
= 150× 15
= 2250 N
Source: https://www.zigya.com/study/book?class=11&board=hbse&subject=Physics&book=Physics+Part+I&chapter=Laws+of+Motion&q_type=&q_topic=Newton%3FS+First+Law+Of+Motion&q_category=&question_id=PHEN11037343
0 Response to "If a Bus Suddenly Stops the Driver s Body Continues to Move Forward"
Post a Comment